The New Ranges Library

A small-time jump, and we are in the year 2020. C++ will get – as far as the future is predictable – the new ranges library. Thanks to Eric Nieblers library, working with the Standard Template Library (STL) will become more comfortable and powerful.

Much more comfortable because the algorithm of the STL can directly work on the containers and need no begin and end iterator. We get more powerful with the ranges library lazy evaluation, improved function composition, and range comprehension in C++20.

Firstly, let me talk about the point more comfortably.

More comfortable

Iterators are the glue between the generic algorithms and containers of the STL. Therefore, each container returns on request an iterator pointing to the first element and an iterator pointing just behind the last element of the container. The half-open range interval defines the range of the algorithm. Thanks to the ranges library, you no longer need a half-open interval in C++20. You can directly apply the algorithm to the container:

std::vector<int> vec{2, 5, 3, 1, 4};
std::sort(vec.begin(), vec.end());   
std::sort(vec);                   // C++20

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Now, I will write about the functional features in the ranges library.

Lazy evaluation

Haskell is, by default, lazy (see Recursion, List Manipulation, and Lazy Evaluation). Due to lazy evaluation, you can define in the Haskell algorithm on infinite data structures if you only ask for a finite number of elements at runtime. Therefore, you can separate the algorithm for calculating the infinite data structure from its usage.

Lazy evaluation is one of the characteristics of functional programming. With C++20, we will get it. Thanks to lazy evaluation, I can directly translate the Haskell code in the example into C++:

// lazyEvaluation.cpp

#include <range/v3/all.hpp>
#include <iostream>
#include <tuple>

using namespace ranges;

int main(){

  std::cout << std::endl;

  // take 5 [1..]  -- [1,2,3,4,5]

  auto num = view::take(view::ints(1), 5);
  ranges::for_each(num, [](int i){ std::cout << i << " "; });

  std::cout << "\n\n";

  auto pairs= view::zip_with([](int i, char c){ return std::make_pair(i, c); } , view::ints(0), "ranges");

  ranges::for_each(pairs, [](std::pair<int,char> p){ std::cout << "(" <<  p.first << ":" << p.second << ")"; });

  std::cout << "\n\n";

}

view::ints(1) in line 15 creates an infinite sequence of numbers starting with 1. The key is that I’m only asking for 5 of them. Using a lambda function, the numbers will be displayed in the following for_each loop. Admittedly, that is not so elegant. Firstly, I can implement the algorithm more elegantly with function composition: auto num= view::ints(1) | view::take(5). The details will follow in a few seconds. Secondly, the upcoming C++20 standard will support the output of ranges with the range-based for-loop: for (n: num) std::cout << num << ” “.

The functional world-known function view::zip_with takes lists and a lambda function and zips the list with the help of a lambda function to a new list. Therefore, the lambda function in line 22 zips the infinite sequence of numbers starting with 0 with the finite string “ranges”. The result is a finite tuple. So you can refer to elements of the pairs by using the first or second.

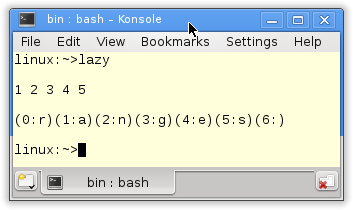
Function composition

Function composition in Haskell feels like putting Lego stones together. The newly created functions express their functionality very concisely and are readable for the used programmer, like prose. In Haskell, the power of function composition is based on three pillars:

Haskell’s functions

perform one task,
use the list as the essential data structure and
use the (.) for function composition.

The story is similar to the ranges library. The library has a rich set of functions. These functions are inspired by Haskell, which works on the key data structure range and uses the, from the Unix shell or Windows PowerShell known, pipe symbol (|) for function composition.

Once more, I show how you can implement Haskell code in C++20:

// functionCompositionRanges.cpp

#include <range/v3/all.hpp>
#include <numeric>
#include <iostream>

using namespace ranges;

int main(){

  std::cout << std::endl;

  // odds= takeWhile (< 1000) . filter odd . map (^2)
  // odds [1..]                 -- [1,9,25, ... , 841,961]

  auto odds= view::transform([](int i){ return i*i;} ) |
             view::remove_if([](int i){ return i % 2 == 0; } ) |
             view::take_while([](int i){ return i < 1000;} );
  auto oddNumbers= view::ints(1) | odds;

  ranges::for_each(oddNumbers,[](int i){ std::cout << i << " "; });

  std::cout << "\n\n";

  // total= sum $ take 100 $ map (\x -> x*x) [100..1000] -- 2318350

  auto total= ranges::accumulate(view::ints(100, 1000) |
                                 view::transform([](int x){ return x*x; }) |
                                 view::take(100), 0);

  std::cout << "total: " << total << std::endl;

  std::cout << std::endl;

}

The evaluation order of function composition is in Haskell (line 13) from right to left; in C++ (lines 16 – 19) from left to right. The C++ expression in lines 27 – 29 is not so easy to digest. It accumulates (ranges::accumulate) the first 100 numbers (view::take(100)) from the numbers from 100 – 1000 (view::ints(100,1000)) by mapping each number to its square (view::transform([](int x){ return x*x; }). The start value is 0.

Here is the output of the program.

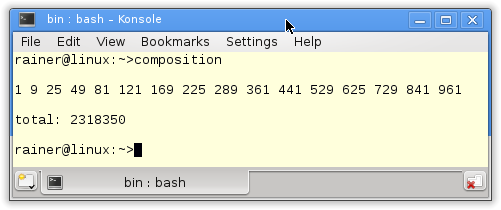
Range comprehension

List comprehension is syntactic sugar of the sweetest kind for the functional algorithm map and filter and allows you to create new lists at runtime. The functional programming language Miranda introduced list comprehension; Haskell made them known. It is not an accident that list comprehension looks like the mathematical notation for set comprehension because Haskell is based on mathematical concepts.

The figure compares set comprehension in Mathematics with list comprehension in Haskell.

The ranges library supports range comprehension. It’s not as sweet as list comprehension, but the functionality is comparable.

// rangeComprehension.cpp

#include <range/v3/all.hpp>
#include <iostream>

using namespace ranges;

int main(){

  std::cout << std::endl;

  // odds= [ x*x | x <-[1..] , odd x  ]
  // takeWhile (<1000) odds --  -- [1,9,25, ... , 841,961]

  auto odds= view::ints(1) | view::for_each([](int i){ return yield_if(i%2 == 1, i*i); });

  ranges::for_each(odds | view::take_while([](int i){ return i < 1000; }) , [](int i){
    std::cout << i << " ";
  });

  std::cout << "\n\n";

}

The list comprehension in Haskell (line 12) is very concise. I request the integers starting with 1(x<-[1..]), keep the odd values (odd x), and map them to their square (x*x). The expression odd corresponds to the filter function and x*x to the map function. The list will be evaluated in line 13 as long as their elements are smaller than 1000 (takeWhile(<1000)).

I apply the same strategy in C++. The first argument of the yield_if function is the filter expression, and the second one is the map expression.

In the end, the output of the program.

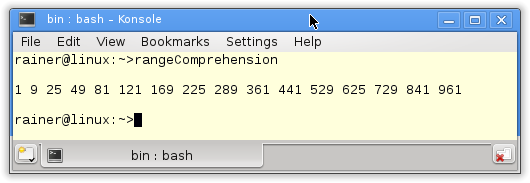
If I use more generators for integers or filter expressions in a range of comprehension, the expression will become very difficult to understand. I present in the following example the Pythagorean Triple in Haskell and C++. The Pythagorean triple consists of three positive integers $x$ , $y$ , and $z$ , such that $x 2 + y 2 = z 2$ .

triples =[(x, y, z)|z <-[1..], x <-[1..z],y <-[x..z] ,x^2 + y^2 == z^2]

auto triples = 
  view::for_each(view::ints(1),[](int z){
    return view::for_each(view::ints(1, z),[=](int x){
      return view::for_each(view::ints(x, z),[=](int y){
        return yield_if(x*x + y*y == z*z, std::make_tuple(x, y, z));
      });
    });
  });

The view algorithms, such as view::for_each of the ranges library, are standard in that they are lightweight wrappers for the underlying range. They will only evaluate its arguments on request and can not change them. With actions such as (action::remove_if), the ranges library has a bunch of additional algorithms that can change their arguments and create new ranges. Contrary to the view algorithms, the action algorithms are not lazy. They are eager.

What’s next?

Eric Niebler used the type-traits library to make the range library’s algorithm type-safe. That is no longer necessary with C++20 because we get concepts. Now you know what I will write about in my next post.

Post Views: 5,639

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS