From Variadic Templates to Fold Expressions

In my last two posts, “Variadic Templates or the Power of Three Dots” and “More about Variadic Templates“, I introduced variadic templates. This post goes one step further in the future, and presents fold expressions that can directly reduce a parameter pack with a binary operator.

I intentionally skipped one import use case for variadic templates: the perfect factory function. When you combine perfect forwarding with variadic templates, you get the perfect factory function. The perfect factory function is a function that can accept an arbitrary number of arguments of any value category (lvalue or rvalue). Curious? Read my previous post, “C++ Core Guidelines: Rules for Variadic Templates“.

But now, I want to present something new with fold expressions.

Fold Expressions

C++11 supports variadic templates. These are templates that can accept an arbitrary number of template parameters. A so-called parameter pack holds an arbitrary number. Additionally, with C++17, we got fold expressions. You can directly reduce a parameter pack with a binary operator thanks to fold expressions. Let’s look at reducing an arbitrary number of numbers to a value.

// variadicTemplatesFoldExpression.cpp

#include <iostream>

bool allVar() {                                              // (1)
    return true;
}

template<typename T, typename ...Ts>                         // (2)
bool allVar(T t, Ts ... ts) {                                // (3)
    return t && allVar(ts...);                               // (4)
}

template<typename... Args>                                   // (5)
bool all(Args... args) { return (... && args); }            

int main() {

    std::cout << std::boolalpha;

    std::cout << '\n';

    std::cout << "allVar(): " << allVar() << '\n';
    std::cout << "all(): " << all() << '\n';

    std::cout << "allVar(true): " << allVar(true) << '\n';
    std::cout << "all(true): " << all(true) << '\n';

    std::cout << "allVar(true, true, true, false): " 
              << allVar(true, true, true, false) << '\n';
    std::cout << "all(true, true, true, false): " 
              << all(true, true, true, false) << '\n';

    std::cout << '\n';

}

Both function templates allVar and all return at compile time if all arguments are true. allVar uses variadic templates; all fold expressions.

The variadic templates allVar applies recursion to evaluate its arguments. The function allVar (1) is the boundary condition if the parameter pack is empty. The recursion takes place in the function template allVar (2). The three dots stand for the so-called parameter pack. Parameter packs support two operations. You can pack or unpack them. It is packed in line (2); unpacked in (3) and (4).

Line (4) requires our full attention. Here, the head of the parameter pack t is combined with the rest ts of the parameter pack ts using the binary operator &&. The call allVar(ts …) triggers the recursion. The call includes a parameter pack that is the original one reduced by the head. Fold expressions (5) make our job easier. With fold expressions, you can directly reduce the parameter pack with the help of the binary operator: (... && args).

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Here is the output of the program.

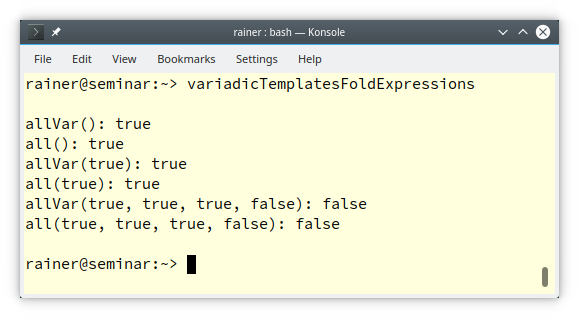
A fold expression applies a binary operator to a parameter pack.

Application of the binary Operator

A fold expression can apply the binary operator in two different ways.

With and without an initial value.
Fold the variadic pack from left or from right

There is a subtle difference between the algorithm allVar and all. All have the default value true for the empty parameter pack.

C++17 supports 32 binary operators in fold expressions: “+ – * / % ^ & | = < > << >> += -= *= /= %= ^= &= |= <<= >>= == != <= >= && || , .* ->*” . A few of them have default-values:

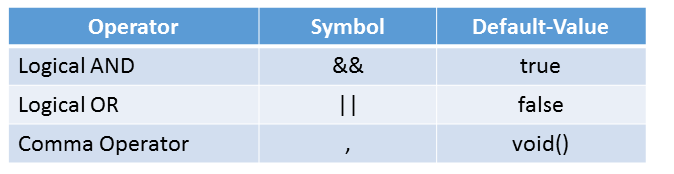
You must provide an initial value for binary operators with no default value. You can specify an initial value for binary operators with a default value.

If the ellipsis stands left of the parameter pack, the parameter pack will be processed from the left. If right of the parameter pack, it will be processed from the right. This is also true if you provide an initial value.

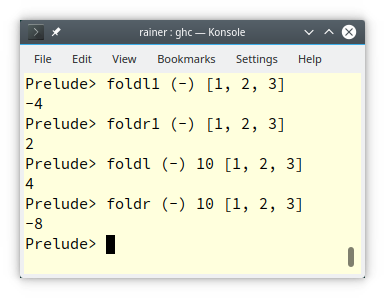
Fold expression allows it to implement Haskell functions foldl, foldr, foldl1, and foldr1 directly in C++.

A Flavor of Haskell

The following table shows the four variations of fold expression and their Haskell pendants. The C++17 standard requires that fold expressions with initial value use the same binary operator op.

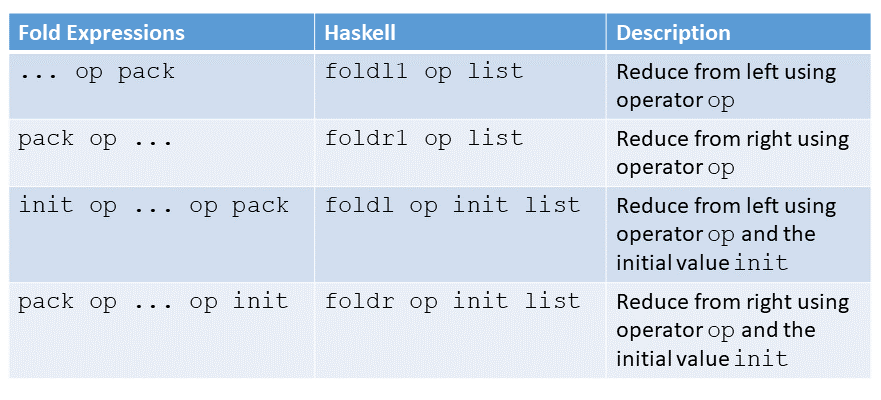
The C++ and Haskell variations differ in two points. The C++ version uses the default value as the initial value; the Haskell version uses the first element as the initial value. The C++ version processes the parameter pack at compile time, and the Haskell version processes its list at run time.

The following program shows all four variations of fold expression. Each one subtracts a few numbers.

// foldVariations.cpp

#include <iostream>

template<typename... Args>                   // (1)
auto diffL1(Args const&... args) {
    return (... - args);
}

template<typename... Args>                   // (2)
auto diffR1(Args const&... args) {
    return (args - ...);
}

template<typename Init, typename... Args>    // (3)
auto diffL(Init init, Args const&... args) {
    return (init - ... - args);
}

template<typename Init, typename... Args>    // (4)
auto diffR(Init init, Args const&... args) {
    return (args - ... - init);
}

int main() {

    std::cout << '\n';

    std::cout << "diffL1(1, 2, 3): " << diffL1(1, 2, 3) << '\n';       // (1 - 2) - 3
    std::cout << "diffR1(1, 2, 3): " << diffR1(1, 2, 3) << '\n';       // 1 - (2 - 3)
    std::cout << "diffL(10, 1, 2, 3): " << diffL(10, 1, 2, 3) << '\n'; // ((10 - 1) - 2) - 3
    std::cout << "diffR(10, 1, 2, 3): " << diffR(10, 1, 2, 3) << '\n'; // 1 - (2 - (3 - 10))

    std::cout << '\n';

}

The functions diffL1 (1) and diffL (3) process the numbers from the left and the functions diffR1 (2) and diffR (3) process them from the right. Additionally, the functions diffL and diffR use an initial start value. The comments in the main function shows the processing steps.

I execute the Haskell pendant directly in the Haskell shell.

What’s next?

Variadic templates, mainly fold expressions, enable concise expressions to be written for repeated operations. Learn more about it in my next post.

Post Views: 5,337

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery,and Matt Godbolt.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS