Avoiding Temporaries with Expression Templates

Expression templates are typically used in linear algebra and are “structures representing a computation at compile-time, which are evaluated only as needed to produce efficient code for the entire computation” (https://en.wikipedia.org/wiki/Expression_templates). In other words, expression templates are only evaluated when needed.

I provide you with this post only the critical ideas of expression templates. To use them, you should study further content, such as

C++ Templates: The Complete Guide by David Vandervoorde, Nicolai M. Josuttis, and Douglas Gregor (http://www.tmplbook.com/)
Boost Basic Linear Algebra Library (https://www.boost.org/doc/libs/1_59_0/libs/numeric/ublas/doc/index.html)
Expression Templates Revisited by Klaus Iglberger (https://www.youtube.com/watch?v=hfn0BVOegac). Klaus’s talk demystifies many performance-related myths about expression templates.

What problem do expression templates solve? Thanks to expression templates, you can get rid of superfluous temporary objects in expressions. What do I mean by superfluous temporary objects? My implementation of the class MyVector.

A first naive Approach

MyVector is a simple wrapper for a std::vector<T>. The wrapper has two constructors (lines 1 and 2), knows its length (line 3), and supports the reading (line 4) and writing (line 4) by index.

// vectorArithmeticOperatorOverloading.cpp

#include <iostream>
#include <vector>

template<typename T>
class MyVector{
  std::vector<T> cont;   

public:
  // MyVector with initial size
  MyVector(const std::size_t n) : cont(n){}                                           // (1)

  // MyVector with initial size and value
  MyVector(const std::size_t n, const double initialValue) : cont(n, initialValue){}  // (2)
  
  // size of underlying container
  std::size_t size() const{                                                           // (3)
    return cont.size(); 
  }

  // index operators
  T operator[](const std::size_t i) const{                                            // (4)
    return cont[i]; 
  }

  T& operator[](const std::size_t i){                                                 // (5)
    return cont[i]; 
  }

};

// function template for the + operator
template<typename T> 
MyVector<T> operator+ (const MyVector<T>& a, const MyVector<T>& b){                   // (6)
  MyVector<T> result(a.size());
  for (std::size_t s = 0; s <= a.size(); ++s){
    result[s] = a[s] + b[s];
  }
  return result;
}

// function template for the * operator
template<typename T>
MyVector<T> operator* (const MyVector<T>& a, const MyVector<T>& b){                  // (7)
   MyVector<T> result(a.size());
  for (std::size_t s = 0; s <= a.size(); ++s){
    result[s] = a[s] * b[s]; 
  }
  return result;
}

// function template for << operator
template<typename T>
std::ostream& operator<<(std::ostream& os, const MyVector<T>& cont){                 // (8)
  std::cout << '\n';
  for (int i = 0; i < cont.size(); ++i) {
    os << cont[i] << ' ';
  }
  os << '\n';
  return os;
} 

int main(){

  MyVector<double> x(10, 5.4);
  MyVector<double> y(10, 10.3);

  MyVector<double> result(10);
  
  result = x + x + y * y;
  
  std::cout << result << '\n';
  
}

Thanks to the overloaded + operator (line 6), the overloaded * operator (line 7), and the overloaded output operator (line 8) the objects x, y, and result behave like numbers.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Why is this implementation naive? The answer is in the expression result = x + x + y * y. To evaluate the expression, three temporary objects are needed to hold the result of each arithmetic expression.

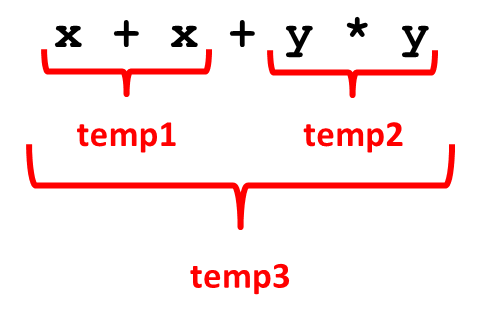
How can I get rid of the temporaries? The idea is simple. Instead of performing the vector operations greedy, I lazily create the expression tree for result[i] at compile time. Lazy evaluation means that an expression is only evaluated when needed.

Expression templates

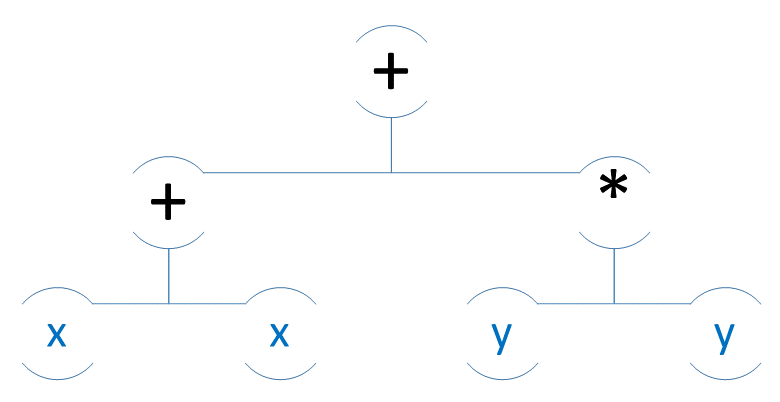
There are no temporaries needed for the expression result[i] = x[i] + x[i] + y[i] * y[i]. The assignment triggers the evaluation. Sadly, the code is, even in this simple usage, not so easy to digest.

// vectorArithmeticExpressionTemplates.cpp

#include <cassert>
#include <iostream>
#include <vector>

template<typename T, typename Cont= std::vector<T> >
class MyVector{
  Cont cont;   

public:
  // MyVector with initial size
  MyVector(const std::size_t n) : cont(n){}

  // MyVector with initial size and value
  MyVector(const std::size_t n, const double initialValue) : cont(n, initialValue){}

  // Constructor for underlying container
  MyVector(const Cont& other) : cont(other){}

  // assignment operator for MyVector of different type
  template<typename T2, typename R2>                                      // (3)
  MyVector& operator=(const MyVector<T2, R2>& other){
    assert(size() == other.size());
    for (std::size_t i = 0; i < cont.size(); ++i) cont[i] = other[i];
    return *this;
  }

  // size of underlying container
  std::size_t size() const{ 
    return cont.size(); 
  }

  // index operators
  T operator[](const std::size_t i) const{ 
    return cont[i]; 
  }

  T& operator[](const std::size_t i){ 
    return cont[i]; 
  }

  // returns the underlying data
  const Cont& data() const{ 
    return cont; 
  }

  Cont& data(){ 
    return cont; 
  }
};

// MyVector + MyVector
template<typename T, typename Op1 , typename Op2>
class MyVectorAdd{
  const Op1& op1;
  const Op2& op2;

public:
  MyVectorAdd(const Op1& a, const Op2& b): op1(a), op2(b){}

  T operator[](const std::size_t i) const{ 
    return op1[i] + op2[i]; 
  }

  std::size_t size() const{ 
    return op1.size(); 
  }
};

// elementwise MyVector * MyVector
template< typename T, typename Op1 , typename Op2 >
class MyVectorMul {
  const Op1& op1;
  const Op2& op2;

public:
  MyVectorMul(const Op1& a, const Op2& b ): op1(a), op2(b){}

  T operator[](const std::size_t i) const{ 
    return op1[i] * op2[i]; 
  }

  std::size_t size() const{ 
    return op1.size(); 
  }
};

// function template for the + operator
template<typename T, typename R1, typename R2>
MyVector<T, MyVectorAdd<T, R1, R2> >
operator+ (const MyVector<T, R1>& a, const MyVector<T, R2>& b){
  return MyVector<T, MyVectorAdd<T, R1, R2> >(MyVectorAdd<T, R1, R2 >(a.data(), b.data()));   // (1)
}

// function template for the * operator
template<typename T, typename R1, typename R2>
MyVector<T, MyVectorMul< T, R1, R2> >
operator* (const MyVector<T, R1>& a, const MyVector<T, R2>& b){
   return MyVector<T, MyVectorMul<T, R1, R2> >(MyVectorMul<T, R1, R2 >(a.data(), b.data()));  // (2)
}

// function template for < operator
template<typename T>
std::ostream& operator<<(std::ostream& os, const MyVector<T>& cont){  
  std::cout << '\n';
  for (int i = 0; i < cont.size(); ++i) {
    os << cont[i] << ' ';
  }
  os << '\n';
  return os;
} 

int main(){

  MyVector<double> x(10,5.4);
  MyVector<double> y(10,10.3);

  MyVector<double> result(10);
  
  result= x + x + y * y;                                                        
  
  std::cout << result << '\n';
  
}

The key difference between the first naive implementation and this implementation with expression templates is that the overloaded + and + operators return in the case of the expression tree proxy objects. These proxies represent the expression trees (lines 1 and 2). The expression trees are only created but not evaluated. Lazy, of course. The assignment operator (line 3) triggers the evaluation of the expression tree that needs no temporaries.

The result is the same.

Thanks to the compiler explorer, I can visualize the magic of the program vectorArithmeticExpressionTemplates.cpp.

Under the hood

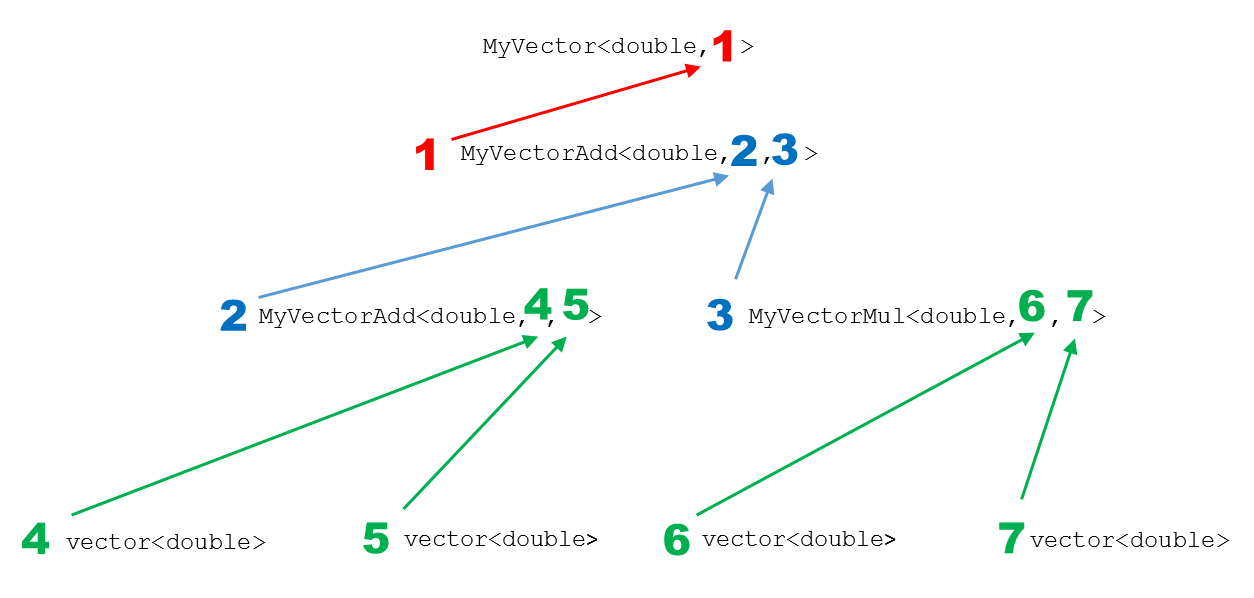
Here are the essential assembler instructions for the final assignment in the main function: result= x + x + y * y.

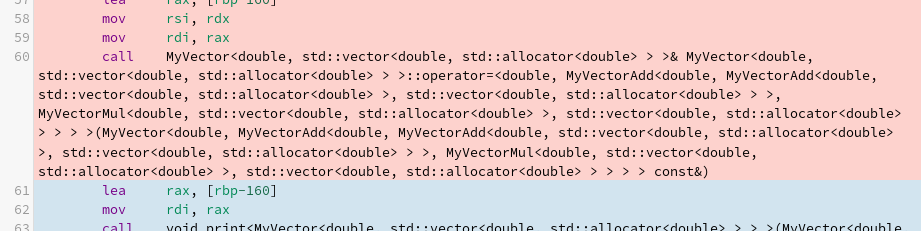
The expression tree in the assembler snippet looks scary, but you can see the structure with a sharp eye. For simplicity reasons, I ignored std::allocator in my graphic.

What’s next?

A policy is a generic function or class whose behavior can be configured. Let me introduce them in my next post.

Post Views: 3,472

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS