C++23: Ranges Improvements and std::generator

C++20 does not provide concrete coroutines, but C++20 provides a framework for implementing coroutines. This changes with C++23. std::generator is the first concrete coroutine.

std::generator is part of the extension of the ranges library in C++23. So, let me start this post with the ranges library in C++20 and its extension in C++23. I will make this short. I already wrote about the ranges library in C++20 and its extension in C++23:

There is only one story I want to complete.

Python’s range function in C++23

In my posts “C++20: Pythonic with the Ranges Library” and “C++20: Pythons range Function“, I implemented Pythons’s 2 range function with the ranges library. The difference between Python’s 2 and Python’s 3 range function is that the 2 version is eager, but the 3 version is lazy. This means that the 2 version creates the numbers, but the 3 version returns a generator to create the numbers on request. I could only solve the challenge in C++20 by using the range-v3 library from Eric Niebler. In particular, I needed the function stride(N), that advanced over another view and returns the N element each time.

std::ranges::views::stride is part of C++23, and the GCC and MSVC compilers support it. Additionally, I use in this example the convenience function std::ranges::to. This C++23 function enables you to construct containers and strings from ranges. Only the MSVC and Clang compilers support this function.

Finally, here is Python’s range function in C++.

// rangeCpp23.cpp

#include <iostream>
#include <ranges>
#include <vector>

std::vector<int> range(int begin, int end, int stepsize = 1) {
    std::vector<int> result{};
    if (begin < end) {                                  // (5)                                
        auto boundary = [end](int i){ return i < end; };
        result = std::ranges::views::iota(begin) | std::views::stride(stepsize) 
                                                 | std::views::take_while(boundary) 
                                                 | std::ranges::to<std::vector>();
    }
    else {                                              // (6)                                  
        begin++;
        end++;
        stepsize *= -1;
        auto boundary = [begin](int i){ return i < begin; };
        result = std::ranges::views::iota(end) | std::views::take_while(boundary) 
                                               | std::views::reverse 
                                               | std::views::stride(stepsize) 
                                               | std::ranges::to<std::vector>();
    }
    return result;
} 
        
int main() {
    
    std::cout << std::endl;

    // range(1, 50)                                 // (1)
    auto res = range(1, 50);
    for (auto i: res) std::cout << i << " ";
    
    std::cout << "\n\n";
    
    // range(1, 50, 5)                              // (2)
    res = range(1, 50, 5);
    for (auto i: res) std::cout << i << " ";
    
    std::cout << "\n\n";
    
    // range(50, 10, -1)                           // (3)
    res = range(50, 10, -1);
    for (auto i: res) std::cout << i << " ";
    
    std::cout << "\n\n";
    
    // range(50, 10, -5)                           // (4)
    res = range(50, 10, -5);
    for (auto i: res) std::cout << i << " ";
    
    std::cout << "\n\n";
    
}

The lines (1) to (4) should be pretty obvious, thanks to the program’s output.

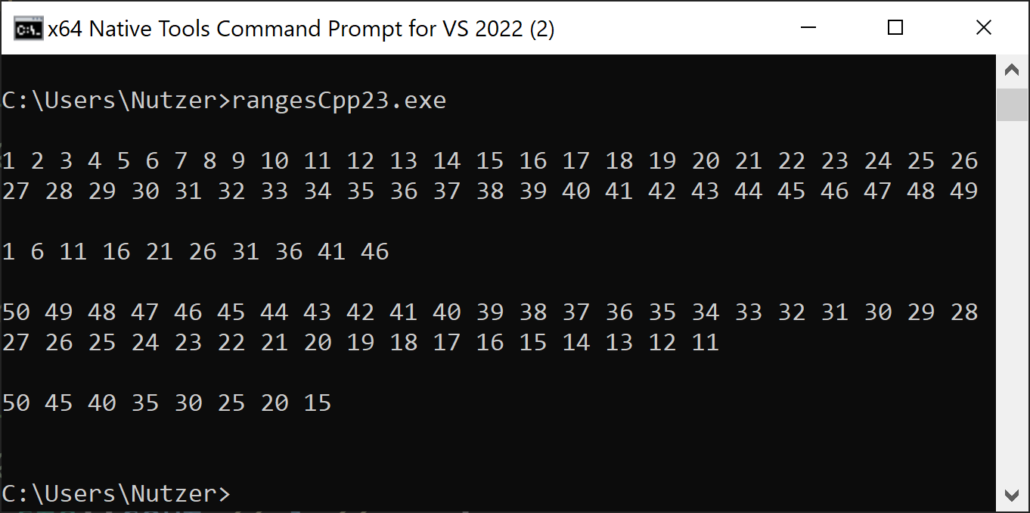
The first two arguments of the range call stand for the beginning and end of the created integers. The begin is included, but not the end. The step size as the third parameter is, per default, 1. The step size should be negative when the interval [begin, end] decreases. If not, you get an empty list or an empty std::vector<int>.

The if condition (begin < end) of the range function in line (5) should be quite easy to read. Create all numbers starting with begin (std::views::iota(begin)), take each n-th element (std::views::stride(stepsize)), and do it as long as the boundary condition holds (std::views::take_while(boundary). Finally, create the std::vector<int>.

I use a little trick in the other case (line 6). I create the numbers [end++, begin++[, take them until the boundary condition is met, reverse them (std::views::reverse), and take each n-th element.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Now, let me jump to first coroutine in C++.

std::generator

std::generator in C++23 is the first concrete coroutine. A std::generator generates a sequence of elements by repeatedly resuming the coroutine from which it was paused.

// generator.cpp

#include <generator>
#include <ranges>
#include <iostream>
 
std::generator<int> fib() {
    co_yield 0;                    // (1)
    auto a = 0;
    auto b = 1;
    for(auto n : std::views::iota(0)) {  
        auto next = a + b;
        a = b;
        b = next;
        co_yield next;            // (2)   
    }
}

int main() {
    for (auto f : fib() | std::views::take(10)) {
        std::cout << f << " ";
    }
}

The function fib is a coroutine. This coroutine creates an infinite stream of Fibonacci numbers. The stream of numbers starts with 0 (line 1) and continues with the following Fibonacci number (line 2). The ranges-based for-loop requests explicitly the first 10 Fibonacci numbers.

So far, no compiler supports std::generator. You can see the coroutine nature of std::generator if you study its header: <generator>.

`std::ranges::elements_of`

std::ranges::elements_of comes into play when you want to call a generator recursively.

std::generator<int> fib() {
    co_yield 0;                    
    auto a = 0;
    auto b = 1;
    for(auto n : std::views::iota(0)) {  
        auto next = a + b;
        a = b;
        b = next;
        co_yield next;               
    }
}

std::generator<int> outer() {
    yield fib();                         // (1)
    yield std::ranges::elements_of(fib); // (2)
}

The outer generator returns in line (1) the inner std::generator<int>, but in line (2) the values of the inner generator. Both coroutines have the same return type.

std::bind_back

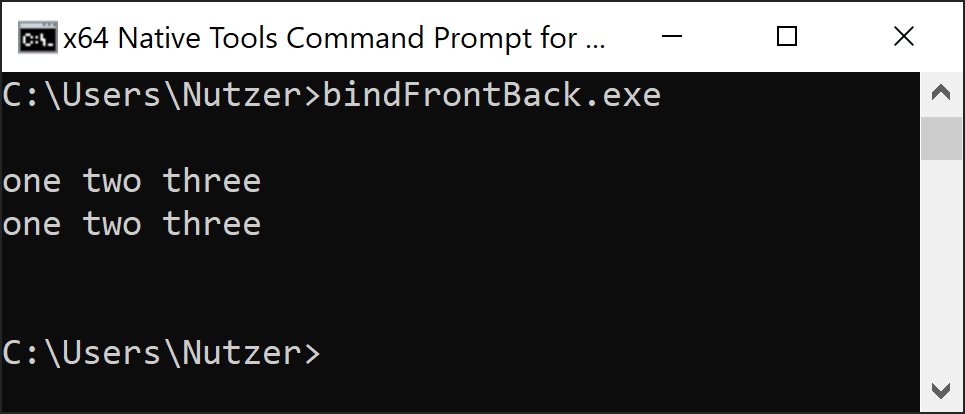
Accordingly, to std::bind_front in C++20, C++23 supports std::bind_back. The following program bindFrontBack.cpp shows the application of both functions.

// bindFrontBack.cpp

#include <functional>
#include <iostream>
#include <string>

int main() {

    std::cout << '\n';
    
    auto add = [](std::string a, std::string b, std::string c) { 
        return a + b + c;
    };

    auto two_three = std::bind_front(add, "one ");
    std::cout << two_three("two ", "three ") << '\n';

    auto one_two = std::bind_back(add, "three ");
    std::cout << one_two("one ", "two ") << '\n';  

    std::cout << '\n';
    
}

Here is the output of the program.

If you want to know more about partial function applications with std::bind, std::bind_front, and std::bind_back, read my post “Partial Function Application“.

What’s next?

I’m done with C++23. Let me jump six years back. In my next post, I will write about an almost unknown feature in C++17: polymorphic allocators.

Post Views: 9,440

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS