Placeholders – The Second

The unification of templates, concepts, and placeholders goes on. This time, I will look closely at constrained (concepts) and unconstrained (auto) placeholders in the context of templates.

First, a short reminder for you (and me). I stated in my last post Concepts -Placeholders: You can use constrained placeholders (concepts) in each situation, whereas you can use unconstrained placeholders (auto). I used in the last post the concept Integral in the algorithm gcd to make it more type-safe. Let’s continue.

Syntactic sugar and more

// conceptsIntegralVariations.cpp

#include <type_traits>
#include <iostream>

template<typename T>
concept bool Integral(){
  return std::is_integral<T>::value;
}

template<typename T>
requires Integral<T>()
T gcd(T a, T b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

template<Integral T>
T gcd1(T a, T b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

Integral gcd2(Integral a, Integral b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

auto gcd3(auto a, auto b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

int main(){

  std::cout << std::endl;

  std::cout << "gcd(100, 10)= "  <<  gcd(100, 10)  << std::endl;
  std::cout << "gcd1(100, 10)= " <<  gcd1(100, 10)  << std::endl;
  std::cout << "gcd2(100, 10)= " <<  gcd2(100, 10)  << std::endl;
  std::cout << "gcd3(100, 10)= " <<  gcd3(100, 10)  << std::endl;

  std::cout << std::endl;

}

Don’t get me wrong. I’m a big fan of syntactic sugar. Syntactic sugar makes a feature easier to use, and you can write more expressive and less error-prone code. Isn’t C++ only syntactic sugar for C or assembler?

I define in lines 7 -9 the concept Integral that I use in the algorithm gcd (lines 11 – 18). Now, I make the syntax sweeter. Instead of specifying the concept in the required clause (line 12), I can use it instead of the keyword typename or class for the type parameter (line 20). It gets even sweeter—the concept Integral is used in line 28 as a function parameter. Of course, gcd2 becomes, by using the concept, a function template. Now the unification kicks in. I will get an unconstrained function template if I replace a constrained placeholder (Integral) in line 28 with the unconstrained placeholders (auto) in line 35. Sorry about my newly coined term, unconstrained function template. I mean, gcd3 is a template that can accept values of arbitrary type.

To wrap up my sentences, here is the output of the program.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

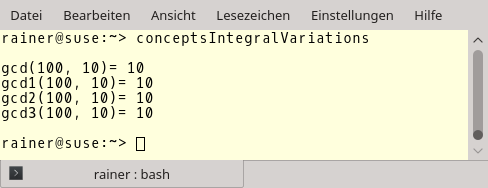
I called this section “Syntactic sugar and more”. But why more? You will see.

Syntactic sugar and more

The function template gcd2 is more potent than the function template gcd or gcd1. gcd2 has two type parameters that have not to be the same. Both have to respect the concept of Integral. The same observations hold for the function template gcd3. a and b have not to be of the same type. Using the function template twoTypes in line 39 makes my point clear.

// placeholders.cpp

#include <iostream>
#include <typeinfo>

template<typename T>
concept bool Integral(){
  return std::is_integral<T>::value;
}

void overload(auto t){
  std::cout << "auto : " << t << std::endl;
}

void overload(Integral t){
  std::cout << "Integral : " << t << std::endl;
}

void overload(long t){
  std::cout << "long : " << t << std::endl;
}
  
void twoTypes(auto a, auto b){
  std::cout << typeid(a).name() << std::endl;
  std::cout << typeid(b).name() << std::endl;
}


int main(){
  
  std::cout << std::endl;
  
  overload(3.14);
  overload(2010);
  overload(2020l);
  
  std::cout << std::endl;
  
  twoTypes(2010, 3.14); 
  
  std::cout << std::endl;

}

With a little bit of Run Time Type Infomation (RTTI) in line 24 and 25, I get a string representation of the types. As expected, the types are int and double.

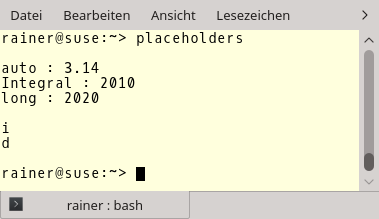
But the short example shows more. The interplay between the unconstrained function template (line 11), the constrained function template (line 15), and the function (line 19) is very smooth. That is precisely the behavior, I expected.

If you hate the classical way of declaring templates, there is a new way.

Template introduction

Instead of declaring your constrained template by using template<Integral T>, you can now just right Integral{T}. Once more, I wrote constrained templates. So, you have to use concepts.

// templateIntroduction.cpp

#include <type_traits>
#include <iostream>

template<typename T>
concept bool Integral(){
  return std::is_integral<T>::value;
}

Integral{T}
Integral gcd(T a, T b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

Integral{T} 
class ConstrainedClass{};

/*

auto{T}
auto gcd(T a, T b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

auto{T} 
class ConstrainedClass{};

*/


int main(){
  
  std::cout << std::endl;
  
  auto res= gcd(100, 10); 

  ConstrainedClass<int> constrainedClass;
  ConstrainedClass<double> constrainedClass1;
  
  std::cout << std::endl;

}

I used the new syntax for the function template gcd in line 11 and the class-template ConstrainedClass in line 19. The concept will kick in if I try to instantiate ConstraintedClass for double (line 45).

I don’t like that I can not replace Integral with auto, such as in lines 24 to 33. In my posts, I have used a constrained placeholder instead of an unconstrained placeholder and the other way around. That is a simple principle.

Of course, I can overcome this restriction by using a concept that constantly evaluates to true.

// templateIntroductionGeneric.cpp

#include <iostream>
#include <string>
#include <typeinfo>
#include <utility>


template<typename T>
concept bool Generic(){
  return true;
}

Generic{T}
Generic gcd(T a, T b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

Generic{T} 
class ConstrainedClass{
public:
  ConstrainedClass(){
    std::cout << typeid(decltype(std::declval<T>())).name() << std::endl;
  }
};


int main(){
  
  std::cout << std::endl;
  
  std::cout << "gcd(100, 10): " << gcd(100, 10) << std::endl;
  
  std::cout << std::endl;
 
  ConstrainedClass<int> genericClassInt;
  ConstrainedClass<std::string> genericClassString;
  ConstrainedClass<double> genericClassDouble;
  
  std::cout << std::endl;

}

Generic (lines 9 – 12) is my concept that returns true for all types. Now, I can unify the syntax and define an unconstrained function template (lines 14 – 20) and an unconstrained class template (lines 22 – 28). Sorry for the expression typeid(decltype(std::declval<T>())).name() in line 26 that works even for a type T without a default constructor. This expression returns the string representation of the type parameter T. Here is the program’s output.

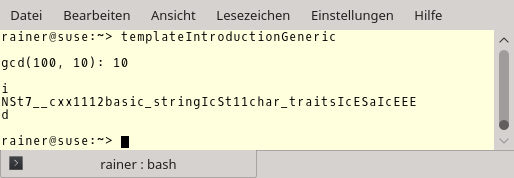
What’s next?

I always use the same concept Integral, in my examples. Bored? That will change. I will write in my next post about defining concepts.

Post Views: 4,995

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery,and Matt Godbolt.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS