Ongoing Optimization: Unsynchronized Access with CppMem

I described my challenge in the last post. Let’s ‘s start with our process of ongoing optimization. To be sure, I verify my reasoning with CppMem. I once made a big mistake in my presentation at Meeting C++ 2014.

To remind you. That is our starting point.

The program

// ongoingOptimization.cpp

#include <iostream>
#include <thread>

int x= 0;
int y= 0;

void writing(){
  x= 2000;
  y= 11;
}

void reading(){ 
  std::cout << "y: " << y << " ";
  std::cout << "x: " << x << std::endl;
}

int main(){
  std::thread thread1(writing);
  std::thread thread2(reading);
  thread1.join();
  thread2.join();
}

Unsynchronized

The program has two data races and therefore has undefined behavior. Either the access to the variable x or the variable y is protected. Because the program has undefined behavior, each result is possible. In C++ jargon, that means a cruise missile can launch, or your PC catches fire. To me, it never happened, but…

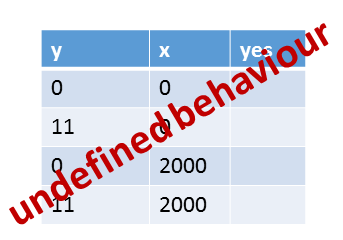
So, we can make no statement about the values of x and y.

It’s not so bad

The known architectures guarantee that the access of an int variable is atomic. But the int variable must be naturally aligned. Naturally aligned means that on a 32-bit architecture, the int variable must have an address divisible by 4. On a 64-bit architecture, divisible by 8. There is a reason why I mention this so explicitly. With C++11, you can adjust the alignment of your data types.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Once more. I don’t say that you should look at int variables as atomics. I only say that the compiler, in this case, guarantees more than the C++11 standard. But, if you use this rule, your program is not compliant with the C++ standard.

This was my reasoning. Now we should look at what CppMem will say about the undefined behavior of the program.

CppMem

int main() {
  int x=0; 
  int y=0;
  {{{ { 
        x= 2000; 
        y= 11;
      }
  ||| {
        y;
        x;
      }  
  }}}
}

The program is reduced to the bare minimum. You can easily define a thread with the curly braces (lines 4 and 12) and the pipe symbol (line 8). The additional curly braces in lines 4 and 7 or lines 8 and 11 define the work package of the thread. Because I’m not interested in the output of the variables x and y, I only read them in lines 9 and 10.

That was the theory for CppMem. Now to the analysis.

Die Analysis

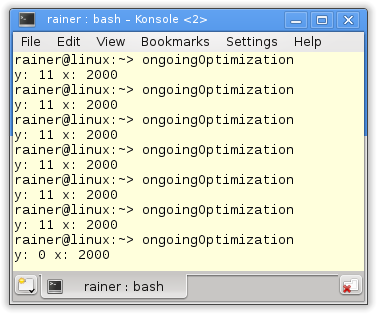
If I execute the program, CppMem complains in the red letters (1), that all four possible interleavings of threads are not race free. Only the first execution is consistent. Now I can use CppMem to switch between the four executions (2) and analyze the annotated graph (3).

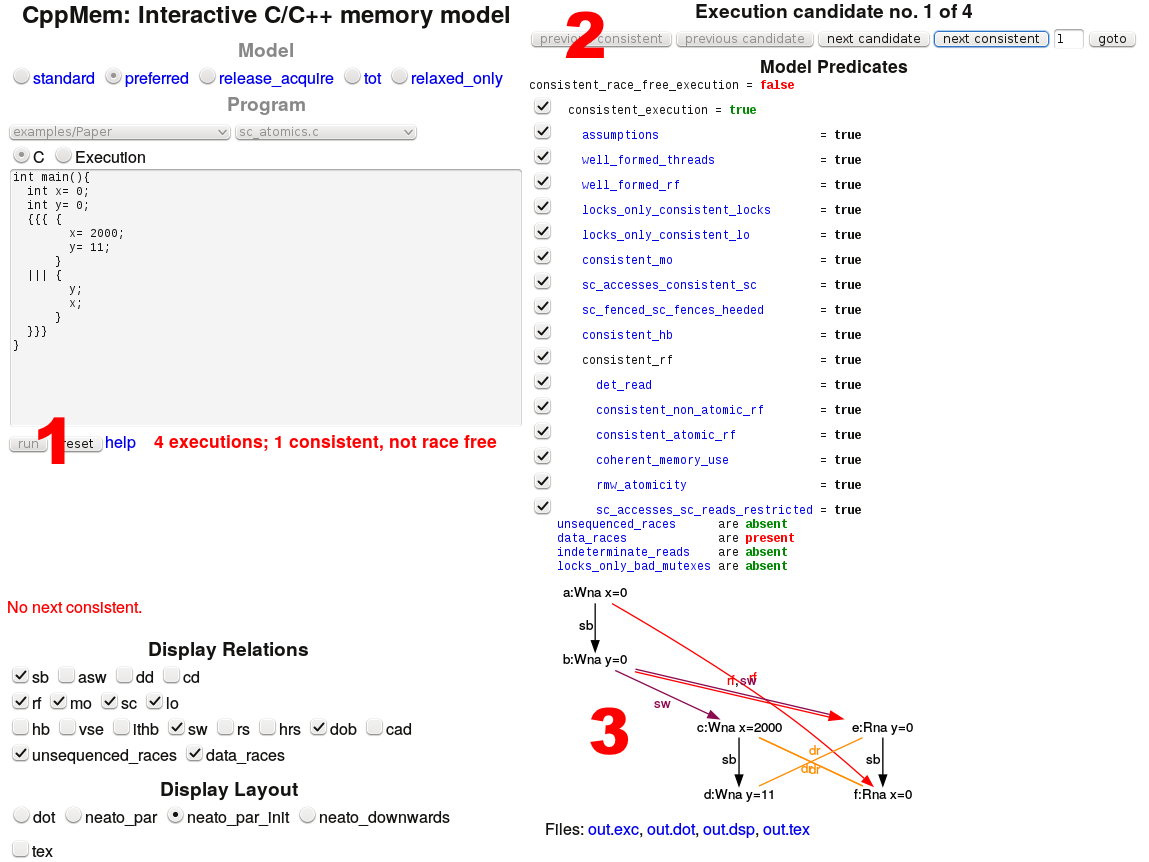
We get the most out of CppMem from the graph. So I will dive more into the four graphs.

First execution

Which information can we draw from paragraph(3)?

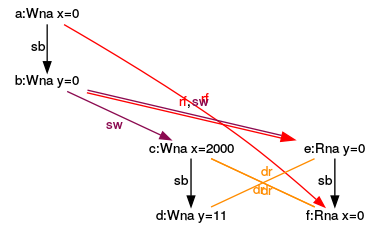
The graph nodes represent the program’s expressions, and the edges represent the expressions’ relations. I will refer in my explanation to the names (a) to (f). So, what can I derive from the annotations in this concrete execution?

a:Wna x=0: Is the first expression (a), a non-atomic write of x.
sb (sequenced-before): The writing of the first expression (a) is sequenced before the writing of the second expression (b). These relations also hold between the expressions (c) and (d) or (e) and (f).
rf (read from): The expression (e) reads the value of y from the expression (b). Accordingly, (f) reads from (a).
sw s(synchronizes-with): The expression (a) synchronizes with (f). This relation holds because the expression (f) occurs in a separate thread. The creation of a thread is a synchronization point. All that happens before the thread creation is visible in the thread. Out of symmetry reasons, the same hold between (b) and (e).
dr (data race): Here is the data race between the reading and writing variables x and y. So the program has undefined behavior.

Why is the execution consistent?

The execution is consistent because the values x and y are read from the values of x and y in the main thread (a) and (b). If the values would be read from x and y from the separate thread in the expressions (c) and (d), the effect can take place that the values of x and y in (e) and (f) are only partially read. This is not consistent. Or to say it differently. In the concrete execution, x and y get the value 0. You can see that in addition to the expressions (e) and (f).

This guarantee will not hold for the subsequent three executions, which I refer to now.

Second execution

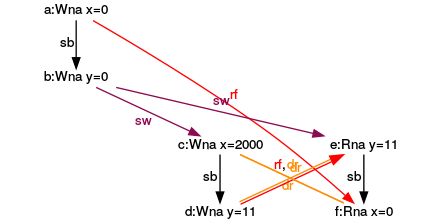
The expression (e) reads in this non-consistent execution the value for y from the expression (d). The writing of (d) will happen parallel to the reading of (e).

Third execution

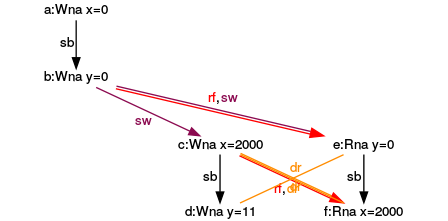
That’s symmetrical to the second execution. The expression (f) reads from the expression (c).

Fourth execution

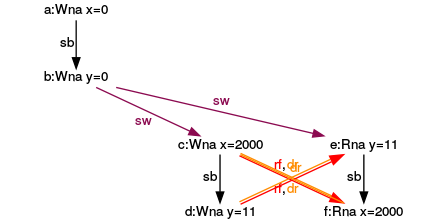
Now all goes wrong. The expressions (e) and (f) read from the expressions (d) and (c).

A short conclusion

Although I just used the default configuration of CppMem and I only used the graph, I get a lot of valuable information and insight. In particular, CppMem brings it right to the spot.

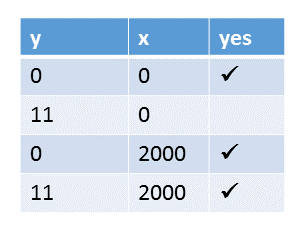
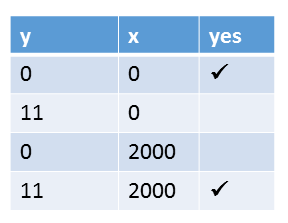
All four combinations of x and y are possible: (0,0), (11,0), (0,2000), (11,2000).
The program has a data race and, therefore, undefined behavior.
Only one of the four executions is consistent.

What’s next?

What is the most obvious way to synchronize a multithreading program? Of course, to use a mutex. This is the topic of the next post.

Post Views: 4,583

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS