Hash Functions

The hash function is responsible for the unordered associative containers’ constant access time (best cast). As ever, C++ offers many ways to adjust the behavior of the hash functions. On the one hand, C++ has a lot of different hash functions; on the other hand, you can define your hash function. You can even adjust the number of buckets.

Before I write about the hash functions, I want to look closer at the declaration of the unordered associative containers. So we will not lose the big picture. I take std::unordered_map as the most prominent unordered associative container.

std::unordered_map

The declaration of the hash table std::unordered_map reveals a lot of exciting details.

template<
    class Key,
    class Val,
    class Hash = std::hash<Key>,
    class KeyEqual = std::equal_to<Key>,
    class Allocator = std::allocator< std::pair<const Key, Val> >
> class unordered_map;

Let’s have a closer look at the template parameters. The std::unordered_map associates the key (Key) with its value (Val). The remaining three template parameters are derived from the key and the value type. This statement holds for the hash function (Hash), the equality function (KeyEqual), and the allocator (Allocator). Therefore, it’s quite easy to instantiate a std::unordered_map char2int.

std::unordered_map<char,int> char2int;

Now it gets more interesting. By default, the hash function std::hash<Key> and the equality function std::equal_to<Key> are used. Therefore, you can instantiate a std::unordered_map with a unique hash or equality function. But stop. Why do we need an equality function? The hash function maps the key to the hash value. The hash value determines the bucket. This mapping can cause a collision. That means different keys go into the same bucket. The std::unorderd_map has to deal with these collisions. To do that, it uses the equality function only for completeness reasons. You can adjust the allocation strategy of the container with the Allocator.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Which requirements have the key and the value of an unordered associative container to fulfill?

The key has to be

comparable with the equality function,
available as a hash value,
copyable and moveable.

The value has to be

default constructible,
copyable and moveable.

{module title=”Mentoring”}

The hash function

A hash function is good if their mapping from the keys to the values produces few collisions and the hash values are uniformly distributed among the buckets. Because the execution time of the hash function is constant, the access time of the elements can also be constant. Instead of that, the access time in the bucket is linear. Therefore, the overall access time of a value depends on the number of collisions in the bucket, respectively.

The hash function

is available for fundamental data types like booleans, integers, and floating points.
is available for the data types std::string and std::wstring,
creates for C string const char* a hash value of the pointer address,
can be defined for user-defined data types.

By applying the theory to my own data types, which I want to use as the key of an unordered associative container, my data type must fulfill two requirements: a hash function and an equality function.

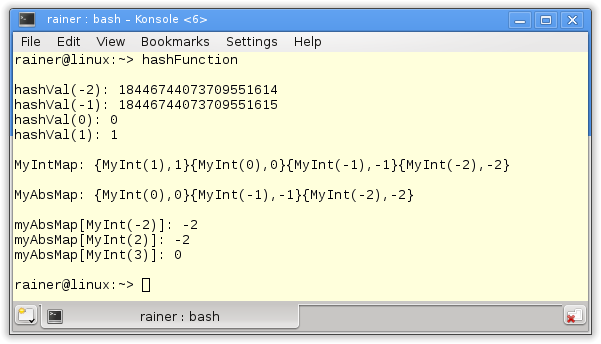
// hashFunction.cpp

#include <iostream>
#include <ostream>
#include <unordered_map>

struct MyInt{
  MyInt(int v):val(v){}
  bool operator== (const MyInt& other) const {
    return val == other.val;
  }
  int val;
};

struct MyHash{
  std::size_t operator()(MyInt m) const {
    std::hash<int> hashVal;
    return hashVal(m.val);
  }
};

struct MyAbsHash{
  std::size_t operator()(MyInt m) const {
    std::hash<int> hashVal;
    return hashVal(abs(m.val));
  }
};

struct MyEq{
  bool operator() (const MyInt& l, const MyInt& r) const {
    return abs(l.val) ==  abs(r.val);
  }
};

std::ostream& operator << (std::ostream& strm, const MyInt& myIn){
  strm << "MyInt(" << myIn.val << ")";
  return strm;
}

int main(){

  std::cout << std::endl;

  std::hash<int> hashVal;

  // a few hash values
  for ( int i= -2; i <= 1 ; ++i){
    std::cout << "hashVal(" << i << "): " << hashVal(i) << std::endl;
  }

  std::cout << std::endl;

  typedef std::unordered_map<MyInt,int,MyHash> MyIntMap;

  std::cout << "MyIntMap: ";
  MyIntMap myMap{{MyInt(-2),-2},{MyInt(-1),-1},{MyInt(0),0},{MyInt(1),1}};

  for(auto m : myMap) std::cout << '{' << m.first << ',' << m.second << '}';

  std::cout << std::endl << std::endl;

  typedef std::unordered_map<MyInt,int,MyAbsHash,MyEq> MyAbsMap;
  std::cout << "MyAbsMap: ";
  MyAbsMap myAbsMap{{MyInt(-2),-2},{MyInt(-1),-1},{MyInt(0),0},{MyInt(1),1}};

  for(auto m : myAbsMap) std::cout << '{' << m.first << ',' << m.second << '}';

  std::cout << std::endl << std::endl;

  std::cout << "myAbsMap[MyInt(-2)]: " << myAbsMap[MyInt(-2)] << std::endl;
  std::cout << "myAbsMap[MyInt(2)]: " << myAbsMap[MyInt(2)] << std::endl;
  std::cout << "myAbsMap[MyInt(3)]: " << myAbsMap[MyInt(3)] << std::endl;

  std::cout << std::endl;

}

My analysis of the program starts with the main function. The easiest way to get the program is to examine the output closely. I create in line 44 the hash function hasVal and use them to calculate the hash values in line 48. hasVal returns a hash value of type std::size_t. std::size_t stands for a sufficiently big enough unsigned integer. MyIntMap in line 53 defines a new name for a type. This type uses MyInt (lines 7 – 13) as a key. Now, MyIntMap needs a hash function and an equality function. It uses MyHash (lines 15 -20) as a hash function. The hash function uses the hash function of the data type int internally. I already overload the equality function for MyInt.

MyAbsMap follows a different strategy. According to its name, MyAbsMap creates its hash value based on the absolute value of the integer (line 25). I use the class MyEq with the overloaded call operator as an equality function. MyEq is only interested in the absolute value of the integer. The output shows that the hash function of MyAbsMap returns the same hash value for different keys. The result is that the hash value for MyInt(-2) (line 70) is identical to the hash value of MyInt(2). This holds although I didn’t initialize MyAbsMap with the pair (MyInt(2),2).

What’s next?

One piece of the puzzle is still missing to understand hash tables better. The hash function maps the key onto the value. Therefore, the hash functions map the key of type int or std::string to its bucket. How is that possible? On the one hand, we have an almost infinite number of keys but only a finite number of buckets. But that is not the only question I have. How many elements go into one bucket? Or to say it differently. How often does a collision occur? Question to which the next post will answer.

Post Views: 7,047

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS