Define Concepts

There are two ways to define a concept: You can combine existing concepts and compile-time predicates, or you can apply a requires expression in four different ways.

Before I write about C++20 and Concepts, I want to remark briefly.

My Second Iteration Through C++20

I have written over 80 posts about C++20 and 20 about Concepts. My previous C++20 posts are one to three years old. This has two important implications. First, I learned, in the meantime, a lot of new stuff about C++20. Second, you don’t have my previous posts in mind. Consequentially, I provide so much content in these posts in my second iteration through C++20 that you can follow my explanation and provide links to my previous posts if necessary.

Following this strategy, here is the general idea of concepts.

Concepts

Generic programming with templates enables it to define functions and classes which can be used with various types. As a result, it is not uncommon for you to instantiate a template with the wrong type. The result can be many pages of cryptic error messages. This problem ends with concepts. Concepts empower you to write requirements for template parameters checked by the compiler and revolutionize how we think about and write generic code. Here is why:

Requirements for template parameters become part of their public interface.
The overloading of functions or specializations of class templates can be based on concepts.
We get improved error messages because the compiler checks the defined template parameter requirements against the template arguments.

Additionally, this is not the end of the story.

You can use predefined concepts or define your own.
The usage of auto and concepts is unified. Instead of auto, you can use a concept.
If a function declaration uses a concept, it automatically becomes a function template. Writing function templates is, therefore, as easy as writing a function.

The following code snippet demonstrates the definition and the use of the straightforward concept Integral:

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

template <typename T>
concept Integral = std::is_integral<T>::value;

Integral auto gcd(Integral auto a, Integral auto b) {
    if( b == 0 ) return a;
    else return gcd(b, a % b);
}

The Integral concept requires from its type parameter T that std::is_integral<T>::value evaluates to true. std::is_integral<T>::value is a function from the type traits library checking at compile time if T is integral. If std::is_integral<T>::value evaluates to true, all is fine; otherwise, you get a compile-time error.

The gcd algorithm determines the greatest common divisor based on the Euclidean algorithm. The code uses the so-called abbreviated function template syntax to define gcd. Here, gcd requires that its arguments and return type support the concept Integral. In other words, gcd is a function template that puts requirements on its arguments and return value. When I remove the syntactic sugar, you can see the nature of gcd.
The semantically equivalent gcd algorithm, using a requires clause.

template<typename T>                                  
requires Integral<T>
T gcd(T a, T b) {
    if( b == 0 ) return a;
    else return gcd(b, a % b);
}

The requires clause states the requirements on the type parameters of gcd.

If you need more information about concepts, read the four following posts:

After this introduction, let me define concepts.

When the concept you are looking for is not one of the predefined concepts in C++20, you must define your concept. I will define a few concepts distinguishable from the predefined concepts through CamelCase syntax. Consequently, my concept for a signed integral is named SignedIntegral, whereas the C++ standard concept goes by the name signed_integral.

The syntax to define a concept is straightforward:

template <template-parameter-list>
concept concept-name = constraint-expression;

A concept definition starts with the keyword template and has a template parameter list. The second line is more interesting. It uses the keyword concept followed by the concept name and the constraint expression.

A constraint-expression is a compile-time predicate. A compile-time predicate is a function that runs at compile time and returns a boolean. This compile-time predicate can either be:

A logical combination of other concepts or compile-time predicates using conjunctions (&&), disjunctions (||), or negations (!)

A requires expression
- Simple requirements
- Type requirements
- Compound requirements
- Nested requirements

Let me continue with the first variant:

A Logical Combination of other Concepts or Compile-Time Predicates

You can combine concepts and compile-time predicates using conjunctions (&&) and disjunctions (||). You can negate components using the exclamation mark (!). Evaluation of this logical combination of concepts and compile-time predicates obeys short-circuit evaluation. Short circuit evaluation means that the evaluation of a logical expression automatically stops when its overall result is already determined.

Thanks to the many compile-time predicates of the type traits library, you have all tools required to build powerful concepts at your disposal.

Let’s start with the concepts Integral, SignedIntegral, and UnsignedIntegral.

template <typename T>           // (1)
concept Integral = std::is_integral<T>::value;

template <typename T>           // (2)
concept SignedIntegral = Integral<T> && std::is_signed<T>::value;

template <typename T>           // (3)
concept UnsignedIntegral = Integral<T> && !SignedIntegral<T>;

I used the type-traits function std::is_integral to define the concept Integral (line 1). Thanks to the function std::is_signed, I refine the concepts Integral to the concept SignedIntegral (line 2). Finally, negating the concept SignedIntegral gives me the concept UnsignedIntegral (line 3). Okay, let’s try it out.

// SignedUnsignedIntegrals.cpp

#include <iostream>

template <typename T>
concept Integral = std::is_integral<T>::value;

template <typename T>
concept SignedIntegral = Integral<T> && std::is_signed<T>::value;

template <typename T>
concept UnsignedIntegral = Integral<T> && !SignedIntegral<T>;

void func(SignedIntegral auto integ) {               // (1)
    std::cout << "SignedIntegral: " << integ << '\n';
}

void func(UnsignedIntegral auto integ) {             // (2)
    std::cout << "UnsignedIntegral: " << integ << '\n';
}

int main() {

    std::cout << '\n';

    func(-5);
    func(5u);

    std::cout << '\n';

}

I use the abbreviated function-template syntax to overload the function func on the concept SignedIntegral (line 1) and UnsignedIntegral (line 2). Read more about the abbreviated function template syntax in my previous post: C++20: Concepts – Syntactic Sugar. The compiler chooses the expected overload: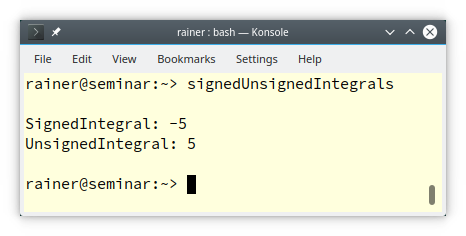

For completeness reasons, the following concept Arithmetic uses disjunction.

template <typename T>
concept Arithmetic = std::is_integral<T>::value || std::is_floating_point<T>::value;

What’s next?

I defined in this post the concepts Integral, SignedIntegral, and UnsignedIntegral using logical combinations of other concepts and compile-time predicates. In my next post, I will apply requires expressions to define concepts.

Post Views: 5,415

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS