C++ Core Guidelines: The Remaining Rules about Performance

Today, I will write about the remaining ten rules of performance. Ten rules seem to be a lot, but only two have content.

Here are the remaining rules to performance:

Let’s have a closer look at rule Per.11 and rule Per.19.

Per.11: Move computation from run time to compile time

The example shows the simple gcd algorithm calculates the greatest common divisior at runtime. gcd uses for its calculation the euclidean algorithm.

int gcd(int a, int b){
    while (b != 0){
        auto t= b;
        b= a % b;
        a= t;
    }
    return a;
}

By declaring gcd as constexpr gcd can quite easily make a function that can run at compile time. There are only a few restrictions on constexpr functions in C++14. gcd must not use static or thread_local variables, exception handling, or goto statements, and all variables must be initialized. Additionally, variables have to be of literal type.

Let’s try it out.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

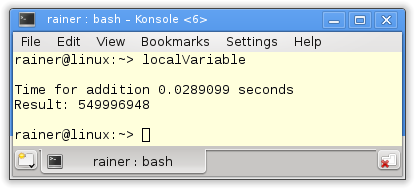
// gcd.cpp

#include <iostream>

constexpr int gcd(int a, int b){
    while (b != 0){
        auto t= b;
        b= a % b;
        a= t;
    }
    return a;
}

int main(){

    std::cout << std::endl;

    constexpr auto res = gcd(121, 11);            // (1)
    std::cout << "gcd(121, 11) = " << res << std::endl;

    auto val = 121;                               // (3)
    auto res2 = gcd(val, 11);                     // (2)
    std::cout << "gcd(val, 11) = " << res2 << std::endl;
  
    std::cout << std::endl;

}

Declaring gcd to a constexpr function does not mean that it has to run at compile time. It means that gcd has the potential to run at compile time. A constexpr function has to be executed at compile if used in a constant expression. (1) is a constant expression because I ask for the result with a contexpr variable res (2). (3) is not a constant expression because res2 is not. When I change res2 to constexpr auto res2, I will get an error: val is not a constant expression. Here is the output of the program.

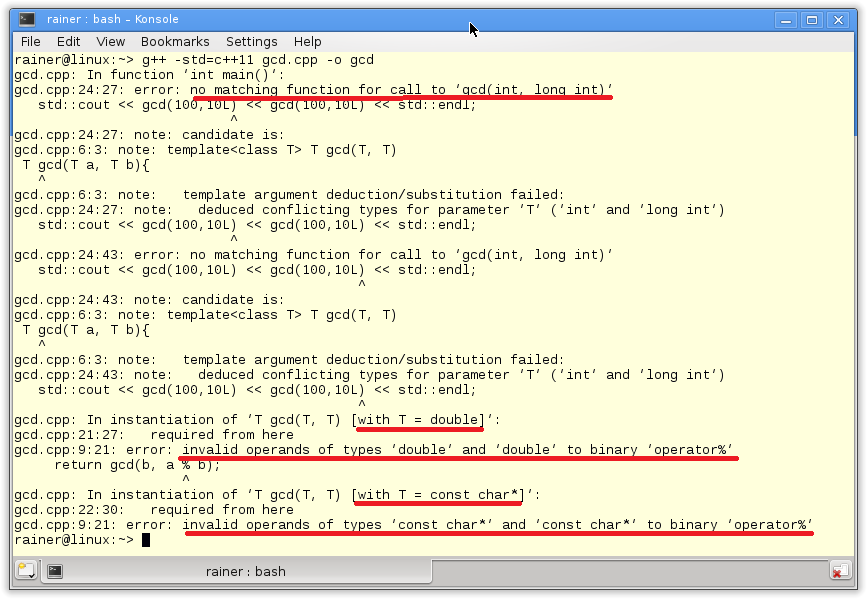
Once more, here is the critical observation. You can use a constexpr function at runtime and at compile time. To use it at compile, its arguments have to be constant expressions.

Don’t believe that line (1) will be executed at compile time? Here is the proof: the assembler instructions to line (1) generated from GCC 7.3 with maximum optimization level. I created the output with the help of the Compiler Explorer from Matt Godbolt.

The function call gcd(121, 11) boils down to its result: 11.

Templates are often used to decide at compile time. There is an excellent example of this idea in the C++ Core Guidelines. A popular technique is to provide a handle for storing small objects on the stack and big objects on the heap. Here is an example:

template<typename T>
struct Scoped {     // store a T in Scoped
        // ...
    T obj;
};

template<typename T>
struct On_heap {    // store a T on the free store
        // ...
        T* objp;
};

template<typename T>
using Handle = typename std::conditional<(sizeof(T) <= on_stack_max),  // (1)
                    Scoped<T>,      // first alternative                  (2)
                    On_heap<T>      // second alternative                 (3)
               >::type;

void f()
{
    Handle<double> v1;                   // the double goes on the stack
    Handle<std::array<double, 200>> v2;  // the array goes on the free store
    // ...
}

How does it work? std::conditional in line (1) is a ternary operator from the type-traits library. In contrast to the ternary operator at runtime (a ? b : c) std::condition will be executed at compile time. This means if std::conditional<(sizeof(T) <= on_stack_max) is evaluated to true, the first alternative is used at runtime. If not, the second alternative.

Per.19: Access memory predictably

What does that mean? If you read an int from memory, more than the size of one int is read from memory. An entire cache line is read from memory and stored in a cache. On modern architectures, a cache line typically has 64 bytes. If you now request an additional variable from memory and this variable is on the previous cache, the read directly uses this cache, and the operation is much faster.

A data structure such as std::vector, which stores its data in a contiguous memory block, is a cache line data structure because each element in the cache line will typically be used. A std::vector has a size and a capacity and can grow only in one direction. The capacity is greater than its size and indicates when it is necessary to allocate memory. This argumentation also applies to std::vector and std::array, although std::array has no capacity.

My argumentation to std::vector will not hold for a std::list or a std::forward_list. Both containers consist of nodes that are double or single-linked.

The std::forward_list can only grow in one direction.

std::deque is in between because it is a double-linked list of small arrays.

This was the theory of cache lines. Now I’m curious. Does it make a difference to read and accumulate all elements from std::vector, a std::deque, std::list, and std::forward_list. The minor program should answer.

// memoryAccess.cpp

#include <forward_list>
#include <chrono>
#include <deque>
#include <iomanip>
#include <iostream>
#include <list>
#include <string>
#include <vector>
#include <numeric>
#include <random>

const int SIZE = 100'000'000; 

template <typename T>
void sumUp(T& t, const std::string& cont){            // (5)
  
  std::cout << std::fixed << std::setprecision(10);

  auto begin= std::chrono::steady_clock::now();
  std::size_t res = std::accumulate(t.begin(), t.end(), 0LL);
  std::chrono::duration<double> last=  std::chrono::steady_clock::now() - begin;
  std::cout << cont <<  std::endl;
  std::cout << "time: " << last.count() << std::endl;
  std::cout << "res: " << res << std::endl;
  std::cout << std::endl;
 
  std::cout << std::endl;
     
}

int main(){
    
    std::cout << std::endl;
    
    std::random_device seed;                            // (1)
    std::mt19937 engine(seed());
    std::uniform_int_distribution<int> dist(0, 100);
    std::vector<int> randNumbers;
    randNumbers.reserve(SIZE);
    for (int i=0; i < SIZE; ++i){
        randNumbers.push_back(dist(engine));
    }
    
    {
      std::vector<int> myVec(randNumbers.begin(), randNumbers.end());
      sumUp(myVec,"std::vector<int>");                 // (2)
    }

    
    {
      std::deque<int>myDec(randNumbers.begin(), randNumbers.end());
      sumUp(myDec,"std::deque<int>");                 // (3)
    }
    
    {
      std::list<int>myList(randNumbers.begin(), randNumbers.end());
      sumUp(myList,"std::list<int>");                 // (4)
    }
    
    {
      std::forward_list<int>myForwardList(randNumbers.begin(), randNumbers.end());
      sumUp(myForwardList,"std::forward_list<int>");  // (5)
    } 
    
}

The program memoryAccess.cpp first creates 100 Million random numbers between 0 and 100 (1). Then it accumulates the elements using a std::vector (2), a std::deque (3), a std::list (4), and a std::forward_list (5). The actual work is done in the function sumUp (6). I assume that Linux and Windows use a pretty similar implementation of std::accumulate; therefore, the access time of the elements is the dominant factor for the overall performance.

template<class InputIt, class T>
T accumulate(InputIt first, InputIt last, T init)
{
    for (; first != last; ++first) {
        init = init + *first;
    }
    return init;
}

I compiled the program with maximum optimization and executed it on Linux and Windows. I’m not interested in the comparison between Linux and Windows because that would be a comparison between a desktop PC and a Laptop. I’m interested in the relative performance numbers of the four containers. Here are they:

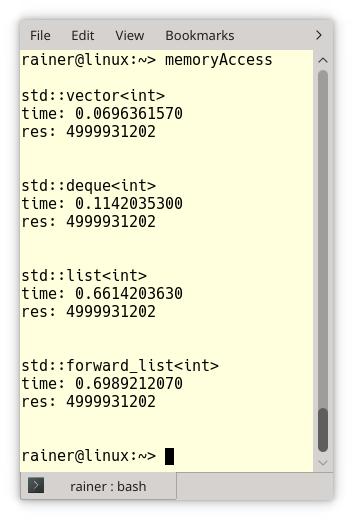
To get the big picture. Here are my observations:

std::vector is 10 times faster than std::list or std::forward_list on Linux and std::vector is 30 times faster than std::list or std::forward_list on Windows.
std::vector is 1.5 times faster than std::deque on Linux, but std::vector is 5 times faster than std::deque on Windows. The reason may be that the double-linked small arrays are bigger on Linux than on Windows. The effect is that the access time is more vectors.
std::deque is 6 times faster than std::list and std::forward_list. This holds for Linux and Windows.
std::list and std::forward_list are in the same ballpark on Linux and Windows.

I don’t want to overestimate my performance numbers, but one key observation is obvious. The more cache line aware the container is, the faster is the access time of the elements: std::vector > std::deque > (std::list, std::forward_list).

What’s next?

That was it to performance. In the next post, I will start to write about the concurrency rules. I’m pretty curious.

Post Views: 4,864

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery,and Matt Godbolt.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS