C++ Core Guidelines: Rules about Statements and Arithmetic

Today, I will write about the remaining rules to statements and the arithmetic rules. If you don’t follow the arithmetic rules, undefined behaviour may kick in.

Four rules to statements are left. Here are they:

The first rule is quite obvious.

ES.84: Don’t (try to) declare a local variable with no name

Declaring a local variable without a name has no effect. With the final semicolon, the variable will go out of scope.

void f()
{
    lock<mutex>{mx};   // Bad
    // critical region
}

Typically, the optimizer can remove the creation of a temporary, if it will not change the observable behavior of the program. This is the so-called as-if rule. To put it the other way around. If the constructor has observable behavior such as modifying the global state of the program, the optimizer is not allowed to remove the creation of the temporary.

ES.85: Make empty statements visible

To be honest, I don’t get the reason for this rule. Why do you want to write empty statements? For me, both examples are just bad.

for (i = 0; i < max; ++i);   // BAD: the empty statement is easily overlooked
v[i] = f(v[i]);

for (auto x : v) {           // better
    // nothing
}
v[i] = f(v[i]);

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

ES.86: Avoid modifying loop control variables inside the body of raw for-loops

Ok. That is, from two perspectives, very bad practice. First, you should avoid writing raw loops and use the algorithms of the Standard Template Library. Second, you should not modify the control variable inside the for-loop. Here is the wrong practice.

for (int i = 0; i < 10; ++i) {
    //
    if (/* something */) ++i; // BAD
    //
}

bool skip = false;
for (int i = 0; i < 10; ++i) {
    if (skip) { skip = false; continue; }
    //
    if (/* something */) skip = true;  // Better: using two variable for two concepts.
    //
}

What makes it difficult for me to reason in particular about the second for-loop is that these are under the hood two nested dependent loops.

ES.87: Don’t add redundant `==` or `!=` to conditions

I’m guilty. In my first years as a professional C++ developer, I often used redundant == or != in conditions. Of course, this changed in the meantime.

// p is not a nullptr
if (p) { ... }            // good
if (p != nullptr) { ... } // redundant 

// p is a nullptr
if (!p) { ... }           // good
if (p == 0) { ... }       // redundant 

for (string s; cin >> s;)  // the istream operator returns bool
v.push_back(s);

These were the rules to statements. Let’s continue with the arithmetic rules. Here are the first seven.

Honestly, there is often not much for me to add to these rules. For completeness (and importance), I will briefly present the rules.

ES.100: Don’t mix signed and unsigned arithmetic

You will not get the expected result if you mix signed and unsigned arithmetic.

#include <iostream>

int main(){

  int x = -3;
  unsigned int y = 7;

  std::cout << x - y << std::endl;  // 4294967286
  std::cout << x + y << std::endl;  // 4
  std::cout << x * y << std::endl;  // 4294967275
  std::cout << x / y << std::endl;  // 613566756
  
}

GCC, Clang, and Microsoft Compiler produced the same results.

ES.101: Use unsigned types for bit manipulation

The reason for the rules is quite simple. Bitwise operations on signed types are implementation-defined.

ES.102: Use signed types for arithmetic

First, you should do arithmetic with signed types. Second, you should not mix signed and unsigned arithmetic. If not, the results may surprise you.

#include <iostream>

template<typename T, typename T2>
T subtract(T x, T2 y){
    return x - y;
}

int main(){
    
    int s = 5;
    unsigned int us = 5;
    std::cout << subtract(s, 7) << '\n';       // -2
    std::cout << subtract(us, 7u) << '\n';     // 4294967294
    std::cout << subtract(s, 7u) << '\n';      // -2
    std::cout << subtract(us, 7) << '\n';      // 4294967294
    std::cout << subtract(s, us + 2) << '\n';  // -2
    std::cout << subtract(us, s + 2) << '\n';  // 4294967294

    
}

ES.103: Don’t overflow, and ES.104: Don’t underflow

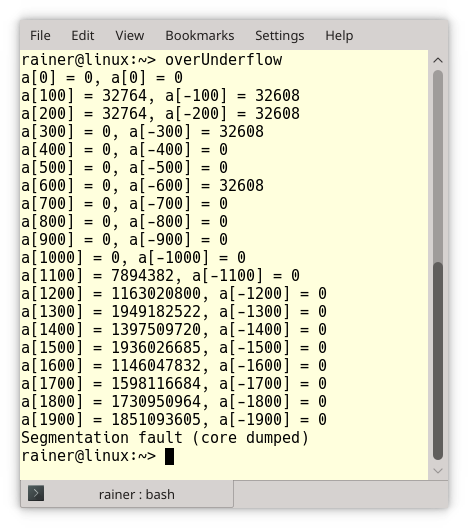
Let me combine both rules. The effect of an overflow or an underflow is the same: memory corruption and undefined behavior. Let’s make a simple test with an int array. How long will the following program run?

// overUnderflow.cpp

#include <cstddef>
#include <iostream>

int main(){
    
    int a[0];
    int n{};

    while (true){
        if (!(n % 100)){
            std::cout << "a[" << n << "] = " << a[n] << ", a[" << -n << "] = " << a[-n] << "\n";
        }
        a[n] = n;
        a[-n] = -n;
        ++n;
    }
    
}

Disturbing long. The program writes each 100th array entry to std::cout.

ES.105: Don’t divide by zero

If you want to have a crash, you should divide by zero. Diving by zero may be fine in a logical expression.

bool res = false and (1/0);

Because the result of the expression (1/0) is not necessary for the overall result, it will not be evaluated. This technique is called short circuit evaluation and is a particular case of lazy evaluation.

ES.106: Don’t try to avoid negative values by using `unsigned`

Don’t use an unsigned type if you want to avoid negative values. The consequences may be severe. Arithmetic behavior will change, and you are open to errors, including signed/unsigned arithmetic.

Here are two examples of the Guidelines, intermixing signed/unsigned arithmetic.

unsigned int u1 = -2;   // Valid: the value of u1 is 4294967294
int i1 = -2;
unsigned int u2 = i1;   // Valid: the value of u2 is 4294967294
int i2 = u2;            // Valid: the value of i2 is -2


unsigned area(unsigned height, unsigned width) { return height*width; } 
// ...
int height;
cin >> height;
auto a = area(height, 2);   // if the input is -2 a becomes 4294967292

As the Guidelines stated, there is an interesting relationship. When you assign a -1 to an unsigned int, you will become the largest unsigned int.

Now to the more interesting case. The behavior of arithmetic will differ between signed and unsigned types.

Let’s start with a simple program.

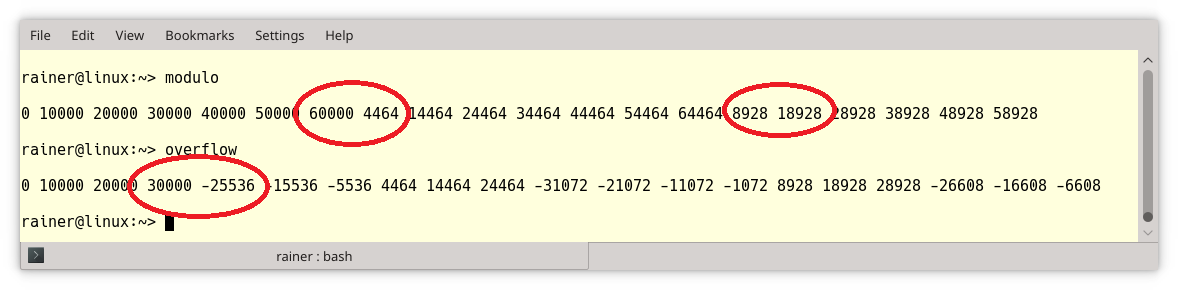
// modulo.cpp

#include <cstddef>
#include <iostream>

int main(){
    
    std::cout << std::endl;
    
    unsigned int max{100000};    
    unsigned short x{0};                 // (2)
    std::size_t count{0};
    while (x < max && count < 20){
        std::cout << x << " ";           
        x += 10000;                      // (1)
        ++count;
    }
    
    std::cout << "\n\n";
}

The key point of the program is that the successive addition to x inline (1) will not trigger an overflow but a modulo operation if the value range of x ends. The reason is that x is of unsigned short (2) type.

// overflow.cpp

#include <cstddef>
#include <iostream>

int main(){
    
    std::cout << std::endl;
    
    int max{100000};    
    short x{0};                     // (2)
    std::size_t count{0};
    while (x < max && count < 20){
        std::cout << x << " ";
        x += 10000;                  // (1)
        ++count;
    }
    
    std::cout << "\n\n";
}

I made a slight change to the program modulo.cpp such that x (2) becomes a signed type. The same addition will now trigger an overflow.

I marked the key points with red circles in the screenshot.

I have a burning question: How can I detect an overflow? Quite easy. Replace the erroneous assignment x += 1000; with an expression using curly braces: x = {x + 1000};. The difference is that the compiler checks narrowing conversions and detects the overflow. Here is the output from GCC.

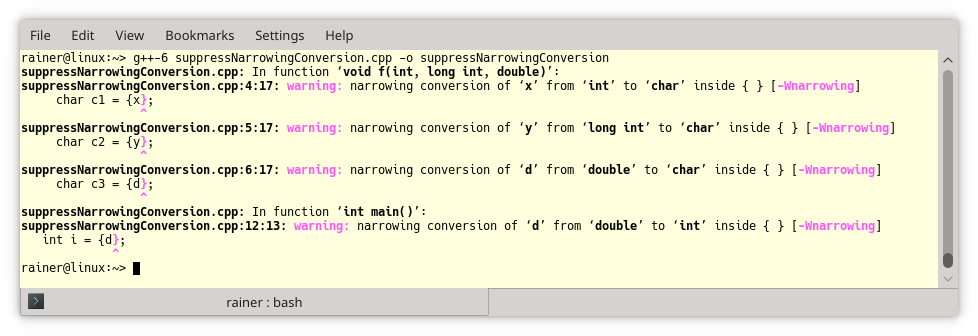
Sure, the expressions (x += 1000) and (x = {x + 1000}) are, from a performance perspective, not the same. The second one could create a temporary for x + 1000. But in this case, the optimizer did a great job, and both expressions were under the hood the same.

What’s next?

I’m nearly done with the arithmetic rules. This means in the next post I will continue my journey with the rules to performance.

Post Views: 4,588

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery,and Matt Godbolt.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS